1)Даны точки А(4;8) В(2;-2) а)найти координаты середины отрезка АВ. б)Найдите длину...

Question

1)Даны точки А(4;8) В(2;-2) а)найти координаты середины отрезка АВ. б)Найдите длину отрезка АВ. в)Определите, какая из данных точек принадлежит прямой х-у+4=0

3)даны точки М(-2;-1) , N(-3;1) , K(0;1) . найдите координаты точки P-? если известно что MNPK-параллелограм. (РЕШИТЕ ПОЖАЛУЙСТА СРОЧНО)

Answer 1

1) Даны точки А(4;8) В(2;-2)
а)  координаты середины М отрезка AB найдем по формуле
Xm = (Xa + Xb)/2, Ym = (Ya + Yb)/2 или  Xm=(4+2)/2=3, Ym=(8-2)/2=3.
Середина отрезка АВ: M(3;3).
б) Длина (модуль) отрезка |АВ|=√((Xb-Xa)² +(Yb-Ya)²) = √((2-4)²+(-2-8)²)=√((-2)²+(-10)²)=√104=2√26.
|AB| = 2√26.
в)Дляопределения, принадлежит ли точка прямой, надо подставить координаты этой точки в уравнение прямой:
для точки А(4;8) => 4-8+4=0  => -4+4=0.
для точки В(2;-2) => 2-2+4=4.
Ответ: точка А(4;8) принадлежит прямой x-y+4=0.
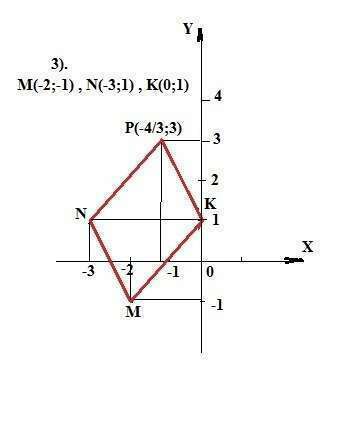
3) В параллелограмме MNKP диагонали делятся точкой пересечения пополам. Найдем координаты этой точки, то есть координаты середины отрезка NK:  O((-3+0)/2;(1+1)/2) или О(-3/2;1).
Зная координаты начала и середины отрезка MP, найдем координаты его конца, точки Р:
Xp=2Xo-Xm = -6/4-(-2) =-2/3+2=4/3=1и1/3.
Yp=2*Yo-Ym= 2-(-1) = 3.
Ответ: Р(4/3;3).

---