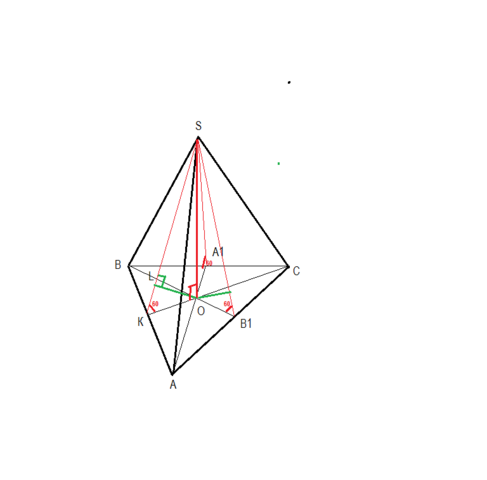
сделаем построение по условию
объем пирамиды V=1/3*So*H
по условию
грани наклонены к основанию под углом 60гр.
LO=2√3 - высота в треугольнике SKO
треугольник SKO -прямоугольный | SO | ┴ (ABC)
треугольник SLO -прямоугольный | OL | ┴ | SK |
OK = LO/sin
высота Н=SO=LO / sin
основание - равносторонний треугольник АВС
все стороны равны, все углы равны 60 град
точка О - центр треугольника , пересечение медиан АА1,ВВ1,СК
известно, что точка О делит медиану в отношении ОК : ОС = 1 : 2
тогда ОК = 1/3 *СК , значит CK = 3*OK = 3*4=12
стороны треугольника АВС АВ=ВС=АС=СК /sin60=12/sin60=8√3
тогда площадь основания
So=1/2*AB*CK=1/2*8√3*12= 48√3
объем пирамиды V=1/3 *48√3 *4√3 = 192
Ответ: 192