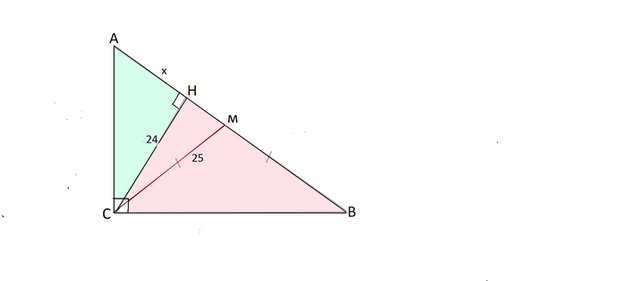
Нарисуем и рассмотрим данный треугольник.
Он прямоугольный.
Медиана прямоугольного треугольника равна половине гипотенузы, следовательно, гипотенуза АВ=2СМ=50 см
Высота СН делит треугольник на два подобных прямоугольных треугольника.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
ПУсть отрезок АН = х см, а НВ=50-х
Тогда:
СН²=АН*НВ
24²=х(50-х)
576=50х -х ²
х²-50х+576=0
Решив квадратное уравнение, получим значения
х₁=18
х₂=32
Из прямоугольных треугольников, на которые высота разбила исходный треугольник АВС, найдем длину катетов.
АС²=АН²+СН²
АС²=576+324=900
АС=30 см
ВС²=СН²+НВ²
ВС²=576+1024=1600
ВС=40
Периметр теперь найти не составит труда:
Р=50+40+30=120 см