Даю 100 баллов. Решите хотя бы одну задачу с рисунком. Задачи: а) Радиус OA окружности с...

Question

Даю 100 баллов.
Решите хотя бы одну задачу с рисунком.
Задачи:
а) Радиус OA окружности с центром O проходит через середину хорды BC. Через точку B проведена касательная к окружности, пересекающая прямую OA в точке M. Докажите, что луч BA – биссектриса угла CBM.
б) Точки A, B и C лежат на окружности, прямая MA – касательная к ней. Докажите, что если точка C равноудалена от прямых AB и AM, то она делит дугу ACB пополам.

Comments

Не выкладывайте заданий со словами "кто сколько может" Ответить могут только два человека, а не полные ответы удаляются по правилам сервиса.

---

А толк то от этого какой будет?Все равно найдутся те люди,которые не все решат.

---

Повторяю: смысл в том, что не полные ответы по правилам сервиса удаляются. То есть те люди, о которых Вы говорите, потеряют баллы за свой ответ. А Вы, к слову , получите их обратно, получив и ответ.

Answer 1

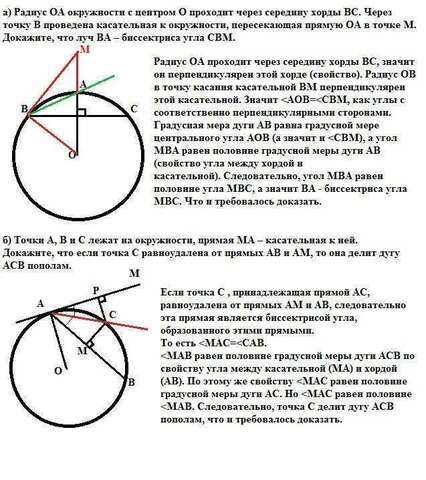
А). Радиус ОА проходит через середину хорды ВС, значит он перпендикулярен этой хорде (свойство). Радиус ОВ в точку касания касательной ВМ перпендикулярен этой касательной. Значит касательной). Следовательно, угол МВА равен половине угла МВС, а значит ВА - биссектриса угла МВС. Что и требовалось доказать.

б). Если точка С , принадлежащая прямой АС, равноудалена от прямых АМ и АВ, следовательно эта прямая является биссектрисой угла, образованного этими прямыми.
То есть <МАВ равен половине градусной меры дуги АСВ по свойству угла между касательной (МА) и хордой (АВ). По этому же свойству <MAC равен половине градусной меры дуги АС. Но <MAC равен половине <МАВ. Следовательно, точка С делит дугу АСВ пополам, что и требовалось доказать.<br>

---