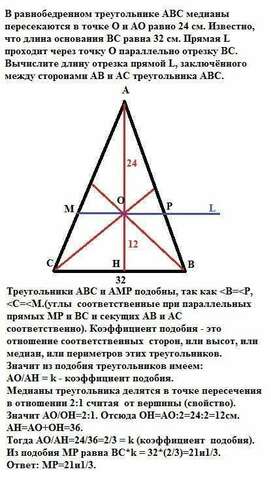
Треугольники АВС и АМР подобны, так как <В=<P, <C=<M (углы соответственные при параллельных прямых МР и ВС и секущих АВ и АС соответственно). Коэффициент подобия - это отношение соответственных сторон, или высот, или медиан, или периметров этих треугольников.<br>Значит из подобия треугольников имеем:
АО/АН = k - коэффициент подобия.
Медианы треугольника делятся в точке пересечения в отношении 2:1 считая от вершины (свойство). Значит АО/ОН=2:1. Отсюда ОН=АО:2=24:2=12см. АН=АО+ОН=36см.
Тогда АО/АН=24/36=2/3 = k (коэффициент подобия).
Из подобия треугольников АВС и АМР: МР равна ВС*k = 32*(2/3)=21и1/3.
Ответ: MP=21и1/3.