В шар вписана правильная треугольная пирамида, длина ребра основания которой равна 6 см. Вычислите расстояние от центра шара до плоскости боковой грани пирамиды, если объём шара равен 256π /3 см³, а его центр расположен внутри пирамиды.
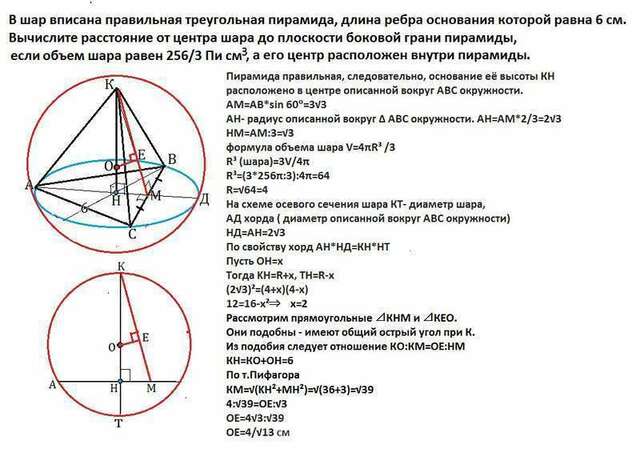
Обозначим пирамиду КАВС, КН - её высота, АД - диаметр окружности, описанной вокруг основания пирамиды - правильного треугольника АВС, АМ - высота ∆ АВС.
Центр шара -О, ОЕ - искомое расстояние- перпендикуляр к грани КВС .
Пирамида правильная, следовательно, основание её высоты КН расположено в центре описанной вокруг АВС окружности, а центр шара лежит на ее высоте.
АМ=АВ*sin 60º=3√3
АН- радиус описанной вокруг ∆ АВС окружности.
АН=АМ*2/3=2√3
НМ=АМ:3=√3
Объём шара V=4πR³ /3
R³ (шара)=3V/4π
R³=(3*256π:3):4π=64
R=∛64=4
На схеме осевого сечения шара КТ- диаметр шара,
АД хорда ( диаметр описанной вокруг АВС окружности)
НД=АН=2√3
По свойству хорд АН*НД=КН*НТ
Пусть ОН=х
Тогда KH=R+x, TH=R-x
(2√3)²=(4+x)(4-x)
12=16-x²⇒
х=2
Рассмотрим прямоугольные ⊿ КНМ и ⊿ КЕО. Они подобны - имеют общий острый угол при К.
Из подобия следует отношение КО:КМ=ОЕ:НМ
КН=КО+ОН=6
По т.Пифагора
КМ=√(KH²+MH²)=√(36+3)=√39
4:√39=ОЕ:√3
OE=4√3:√39
OE=4/√13 см