Жду решение. Все в картинке

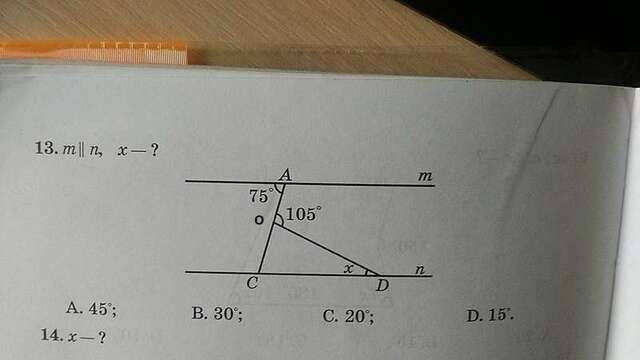
$\angle A = \angle OCD = 75^{\circ}$ , как накрест-лежащие углы при параллельных прямых $m || n$ . Как видно из рисунка, углы $\angle AOD$ и $\angle COD$ — смежные. Сумма смежных углов равна 180°. Отсюда $\angle COD = 180^{\circ} - \angle AOD = 180^{\circ} - 105^{\circ} = 75^{\circ}$
Итого, имеем, что $\triangle CDO$ — равнобедренный с углами $\angle OCD = \angle COD = 75^{\circ}$ , угол $\angle CDO$ — искомый. Найдем его из свойста, что сумма углов треугольника равна 180°:
$\angle OCD + \angle COD + \angle CDO = 180^{\circ} \\ \angle CDO = 180^{\circ} - (\angle OCD + \angle COD) \\ \angle CDO = 180^{\circ} - (2\cdot 75^{\circ}) = 30^{\circ}$
Это ответ.