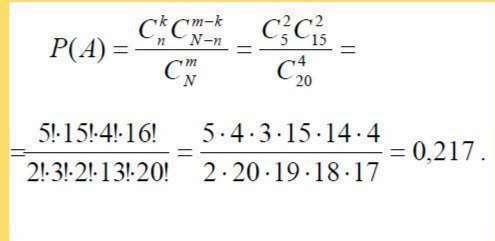Меня интересует ход решения, так как не совсем могу понять что из чего вышло. Если кто может - объясните русским языком. Нижняя строка решения мне не понятна совсем. что от куда взялось?
* В партии из N изделий n изделий имеют скрытый дефект. Какова вероятность
того, что из взятых наугад m изделий k изделий являются дефектными.
N = 20, n = 5, m = 4, k = 2.