** сторонах РК и МН параллелограмма МРКН взяты точки А и В соотвественно,МР=РВ=АК, угол...

Question

на сторонах РК и МН параллелограмма МРКН взяты точки А и В соотвественно,МР=РВ=АК, угол МРВ=60 гр. Найти углы параллелограмма и сравнить отрезки ВМ и АН. Помогите пожалуйста,это билет.....очень нужно....

Answer 1

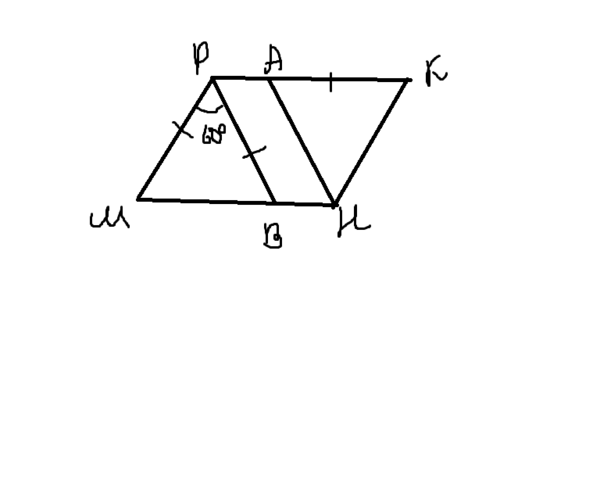
1) Из условия следует, что  ΔМРВ равнобедренный, так как МР=РВ, а если <Р=60, то из этого следует, что  ΔМРВ- равносторонний, так как <М=<В=<img src="https://tex.z-dn.net/?f=%5Cfrac%7B180-60%7D%7B2%7D" id="TexFormula1" title="\frac{180-60}{2}" alt="\frac{180-60}{2}" align="absmiddle" class="latex-formula">=60

2) По свойствам параллелограмма <М=<К=60, <Р=<Н=180-<М=180-60=120( как внутринние односторонние при параллельных РК и МН и секущей МР)</p>

3) Рассмотрим Δ АКН: МР=КН( по свойствам параллелограмма), а по условию АК=МР, из этого следует, что ΔАКН- равнобедренный. Поскольку <К=60, то ΔАКН-равносторонний. Значит МВ=АН</p>

---