В основании прямой треугольной призмы лежит равнобедренный треугольник АВСА1В1С1, у...

Question

В основании прямой треугольной призмы лежит равнобедренный треугольник АВСА1В1С1, у которого АВ=ВС=25 см. , АС=30 см. Через боковое ребро АА1 проведена плоскость, перпендикулярная к ребру ВС. Найти объем призмы, если площадь образовавшегося сечения равна 72 см^2

Answer 1

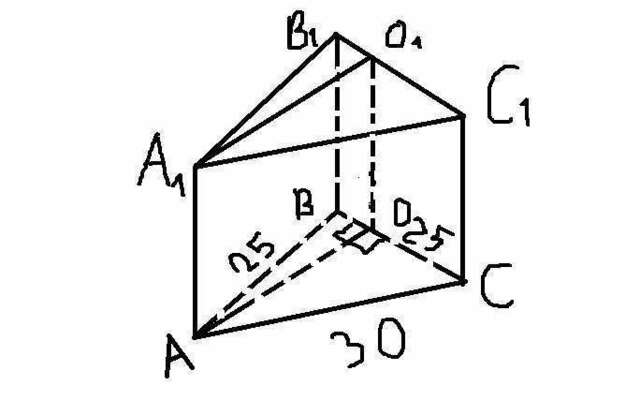
Vпризмы = S(ABC) * AA1

Известна площадь сечения, чтобы найти AA1 найдем AO. Чтобы найти AO наоходим по теореме косинусов угол ABC. cos(ABC)=(AC^2-AB^2-BC^2)/-2AB*BC

cos(ABC)=7/25. Следовательно BO=7, AO=24. AA1=72/24 = 3

Теперь ищем площадь ABC, можно по теореме Герона, но мы нашли BO и OC, поэтому будем находить ее по простейшей формуле. S(ABC)=S(ABO)+S(AOC). S(ABC)=84+216=300

Находим объем призмы. V= S(ABC) * AA1 = 300*3 = 900 см³

---

---