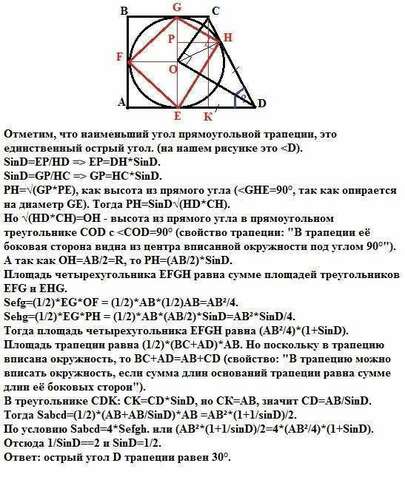
Отметим, что наименьший угол прямоугольной трапеции, это единственный острый угол. (на нашем рисунке это SinD=EP/HD => EP=DH*SinD.
SinD=GP/HC => GP=HC*SinD.
PH=√(GP*PE), как высота из прямого угла (Но √(HD*CH)=OH - высота из прямого угла в прямоугольном треугольнике СOD c Площадь четырехугольника EFGH равна сумме площадей треугольников EFG и EHG.
Sefg=(1/2)*EG*OF = (1/2)*AB*(1/2)AB=AB²/4.
Sehg=(1/2)*EG*PH = (1/2)*AB*(AB/2)*SinD=AB²*SinD/4.
Тогда площадь четырехугольника EFGH равна (AB²/4)*(1+SinD).
Площадь трапеции равна (1/2)*(BC+AD)*AB. Но поскольку в трапецию вписана окружность, то ВС+АD=АВ+СD (свойство: "В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон").
В треугольнике CDK: CK=CD*SinD, но СК=АВ, значит CD=AB/SinD.
Тогда Sabcd=(1/2)*(AB+AB/SinD)*AB =AB²*(1+1/sinD)/2.
По условию Sabcd=4*Sefgh. или (АВ²*(1+1/sinD)/2=4*(AB²/4)*(1+SinD).
Отсюда 1/SinD==2 и SinD=1/2.
Ответ: острый угол D трапеции равен 30°.