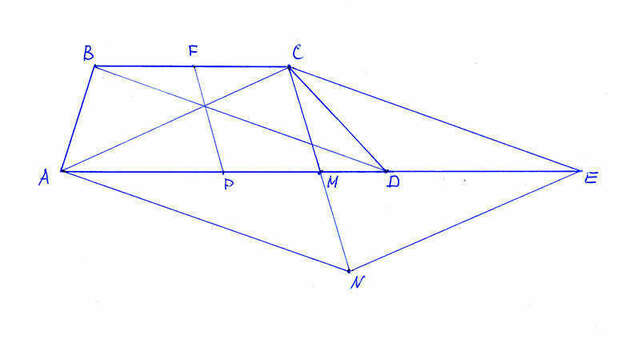
См. чертеж.
DE = BC про построению.
=> BCED - параллелограмм, и CE = BD;
M - середина AE = AD + BC; => PM = (AD + BC)/2 - AD/2 = BC/2 = FC;
=> PFCM - параллелограмм, и CM = FP;
по построению MN = CM; диагонали четырехугольника ACEN делятся точкой пересечения пополам => это тоже параллелограмм.
Площадь трапеции ABCD равна площади треугольника ACE; и та и та равны H*(AD + BC)/2; где H - расстояние от точки C до AD, (в таких случаях говорят, что у треугольника и трапеции общая высота).
Площадь треугольника ACE равна площади треугольника ACN - обе равны половине площади параллелограмма ACEN;
Треугольник ACN имеет стороны 30, 34 и 16; его площадь находится элементарно и равна 240;
Не буду изображать хранителя знаний :)) ACN - прямоугольный треугольник, поскольку 16, 30, 34 - Пифагорова тройка, кратная (8, 15, 17);
Можно было бы и выбрать середину AB - пусть это точка K, и показать, что 1) площадь APK равна 1/4 площади трапеции, достаточно провести среднюю линию, и все видно, 2) APK - (8, 15, 17);