Теорема. Сумма углов произвольного выпуклого n-угольника равна 180° (n-2).
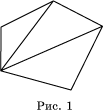
Доказательство. Из какой-нибудь вершины выпуклого многоугольника проведем все его диагонали (рис. 1). Тогда многоугольник разобьется на n-2 треугольника. В каждом треугольнике сумма углов равна 180°, и эти углы составляют углы многоугольника. Следовательно, сумма углов многоугольника равна 180° (n-2).