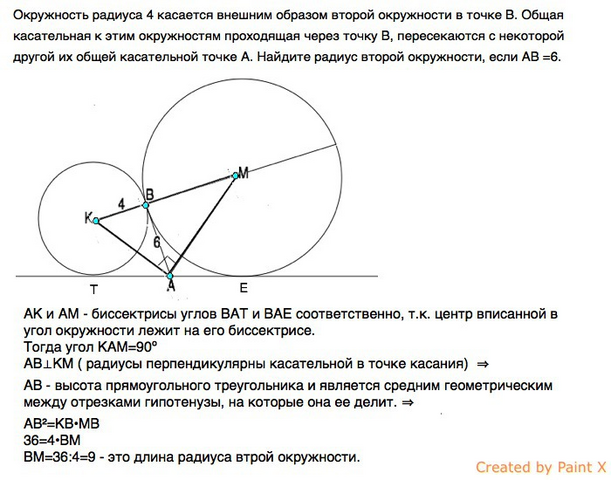
Сделаем рисунок и обозначим центр одной окружности К, второй - М.
Точки касания окружностей со второй касательной Т и Е.
Соединим А с центрами окружностей
АК и АМ - биссектрисы углов ВАТ и ВАЕ соответственно, т.к. центр вписанной в угол окружности лежит на его биссектрисе.
Тогда угол КАМ=90º
АВ⊥КМ ( радиусы перпендикулярны касательной в точке касания)
⇒
АВ - высота прямоугольного треугольника и является средним геометрическим между отрезками гипотенузы, на которые она ее делит. ⇒
АВ²=КВ•MB
36=4•BM
BM=36:4=9 - это длина радиуса второй окружности.