Вычислить интеграл и проверить результат , исходя из его геометрического смысла

$\int\limits^2_1 {(4-2x)} \, dx=(4x-x^{2})|_{1}^{2}=4*2-2^2-4*1+1^2=1$
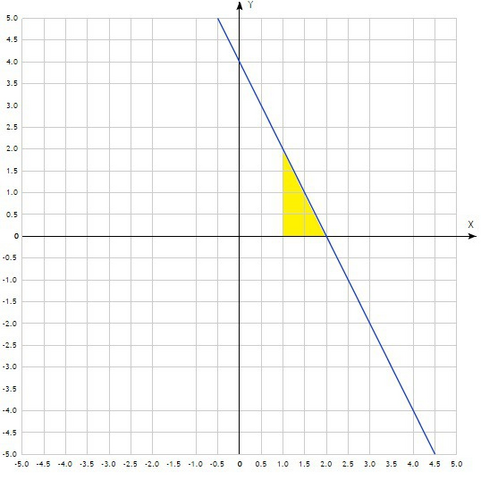
Геометрический смысл интеграла это площадь некоторой фигуры. В приведённом примере фигура ограничена прямой у=4-2х, осью ОХ и линией х=1, эта фигура - прямоугольный треугольник площадь которого 1ед² мы нашли вычислив интеграл.
Площадь прямоугольного треугольника равна половине произведения катетов. Из рисунка находим длину катетов 2 ед. и 1 ед., найдём площадь:
S=(1/2)*2*1=1 ед²
Что и требовалось доказать.