Эта задача дана в эти дни в трех разных вариантах отношения площадей.
Решение мною дано к этому варианту другому пользователю днем раньше.. Это несколько подробнее.
Решение:
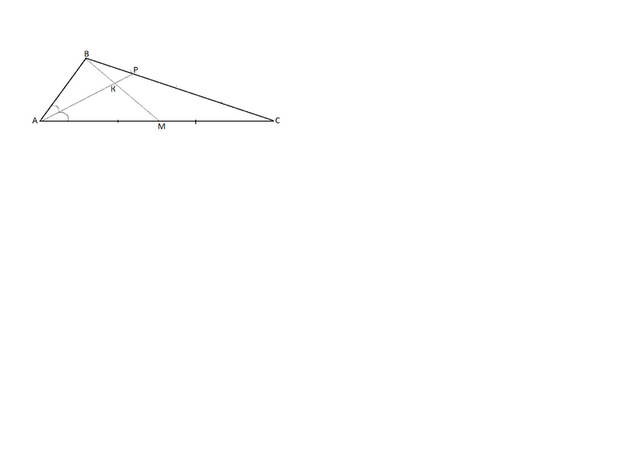
.Сделаем рисунок, стараясь соблюдать по возможности отношение сторон в нем
соразмерным данным задачи.
АС=3 АВ по условию.
АМ=МС - так как ВМ - медиана, и точка М делит АС пополам,
АВ биссектриса и делит угол А пополам. ( В решении равенство углов не пригодится).
Для того, чтобы проще было следить за решением, обозначим площадь ᐃ АВС=S
Площади треугольников с равной высотой и равными основаниями равны.
АМ=МС и равны половине АС, высота треугольников АВМ и ВМС одна и та же,⇒
площадь ᐃ АВМ=площади ᐃ МВС=0,5 S
Биссектриса внутреннего угла треугольника делит противоположную
сторону в отношении, равном отношению двух прилежащих сторон
Следовательно, ВР:РС=АВ:АС=1:3
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Площади Δ ВАР и Δ РАС, имеющих общую высоту из А к ВС, относятся как длины их оснований, т.е
площадь Δ ВАР : Δ РАС.= 1:3
Площадь АВС=S =4 площади треугольника ВАР
( т.к.площадь Δ РАС=3 площади Δ ВАР, всего 4 площади Δ ВАР)
Площадь Δ ВАР=1/4S=0,25 S ( высота Δ ВАР и Δ ВАС одна и та же, а отношение оснований ВР:ВС=1:4))
⇒ площадь Δ РАС =S- 0,25 S = 0, 75 S
Рассмотрим треугольник АВМ.
АК- биссектриса угла АВМ
АМ=АС:2=3 АВ:2=1,5 АВ
Отсюда ВК:КМ=АВ:1,5 АВ (смотри свойство биссектрисы внутреннего угла треугольника)
ВК:КМ=1:1,5
Площадь Δ АВМ= 0,5 S
0,5 S= площадь Δ МАК+ площадь Δ КАВ=2,5 площади Δ КАВ
Площадь Δ BАК=0,5 S:2,5= 0,2 S
Площадь Δ МАК=1,5 площ. Δ КАВ =0,2*1,5= 0,3 S
Площ. МКРС=пл Δ РАС - пл Δ МАК
Площ. МКРС=0,75 S - 0,3 S= 0,45 S
Площадь Δ МАК : площ. МКРС=0,3 S : 0,45 S= 10/15=2/3