Найдите площадь фигуры, ограниченной заданными линиями: у=4-х(во второй степени) У=0 Х=0...

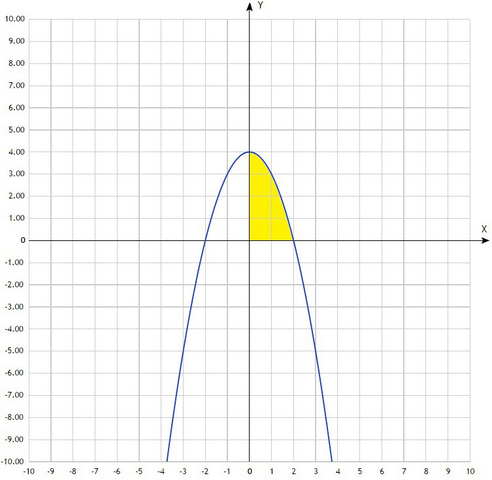
Площадь фигуры это определённый интеграл от функции, ограничивающей эту фигуру. Чертим чертёж (это обязательно). Учитываем, что у=0 это ось ОХ, а х=0 это ось ОY. Из чертежа сразу видно о какой фигуре идёт речь.
На отрезке [0;2] график функции y=4-x² расположен над осью ОХ, поэтому
$S= \int\limits^2_0 {(4-x^2)} \, dx=4x- \frac{x^3}{3}|_{0}^{2}=4*2- \frac{2^3}{3}=8- \frac{8}{3}= \frac{16}{3}=5 \frac{1}{3}$ ед²