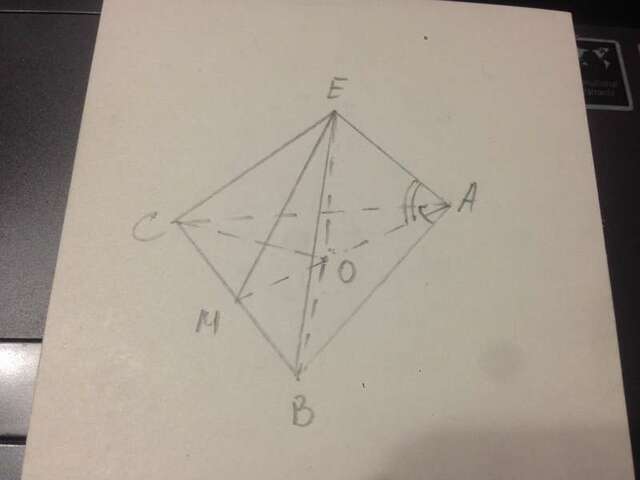
В тр-ке АВС АВ=ВС, ∠ВАС=α. ∠ЕАМ=β, ЕО - высота.
Пусть АВ=АС=х, тогда площадь основания: Sосн=(1/2)х²·sinα.
Так как боковые рёбра одинаково наклонены к плоскости основания, то точка О - центр описанной около основания окружности.
В тр-ке АВМ ∠ВАМ=α/2, АМ=АВ·ctg(α/2)=x·ctg(α/2).
В тр-ке АВС R=АО=АВ·АС/2АМ=х²/(х·ctg(α/2))=x·tg(α/2).
В тр-ке ЕАО ЕО=АО·tgβ=x·tg(α/2)·tgβ.
Площадь тр-ка ЕАМ: Sсеч=АМ·ЕО/2=(1/2)x²·ctg(α/2)·tg(α/2)·tgβ=(1/2)x²·tgβ.
Sсеч:Sосн=[(1.2)х²·tgβ] : [(1/2)x²·sinα]=tgβ:sinα - это ответ.