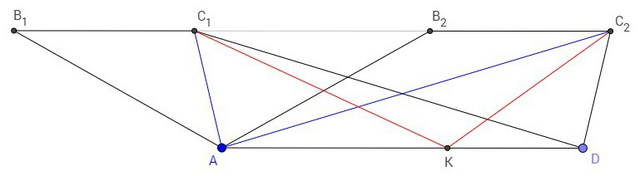
△KCD= SABCD/4
SABCD= (AD+BC)*h/2
AD=2BC
SABCD= 3BC*h/2
△KCD= 3BC*h/8
△KCD= KD*h/2
3BC*h/8 = KD*h/2 <=> KD= 3BC/4
KD= 1,5
AK= 4-1,5 = 2,5
-----
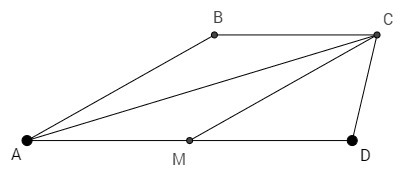
СM - медиана △AСD: AM= 1/2AD =BC
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
СМ=AB
Медиана по трем сторонам: Mc= √(2a^2 + 2b^2 - c^2)/2
CM= √(2AC^2 + 2CD^2 - AD^2)/2
√7= √(2AC^2 + 2CD^2 - 4^2)/2 <=> 7= (AC^2 + CD^2)/2 - 4 <=> AC^2 + CD^2 =22
AD^2= AC^2 + CD^2 -2AC*CD*cos(ACD)
16= AC^2 + CD^2 - AC*CD
16= 22 - AC*CD <=> AC*CD =6
-----
S△ACD= AC*CD*sin(ACD)/2
S△ACD= 3√3/2
S△ACD= AD*h/2
3√3/2 = 4*h/2 <=> h= 3√3/4
-----
S△ACK= AK*h/2
S△ACK= 15√3/16 ~ 1,6237