Центр описанной окружности лежит на пересечении срединных перпендикуляров к сторонам треугольника, следовательно, на высоте равнобедренного ∆ АВС или на ее продолжении.
Ответ зависит от величины угла АВС. Если он тупой, центр О описанной окружности вне треугольника, если острый - внутри него.
Существует формула для радиуса описанной вокруг равнобедренного треугольника окружности. В данном ниже решении она не применялась.
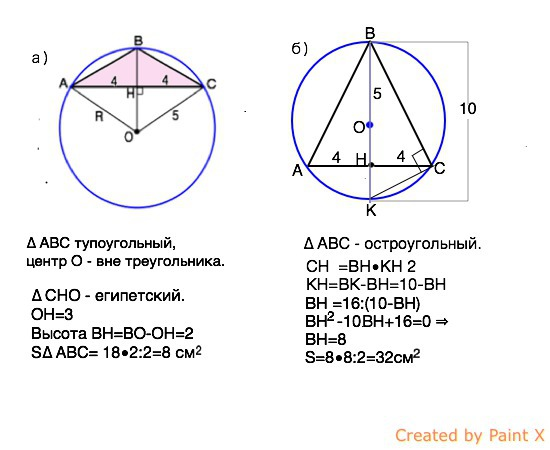
а)∆ АВС тупоугольный, центр О - вне треугольника.
Соединим О с вершинами А и С. Высота ВН еще и медиана и биссектриса ∆ АВС и принадлежит радиусу ВО ( срединному перпендикуляру).
Тогда АН=СН-4
∆ ОНС - «египетский», ⇒ ОН=3 см, ⇒ ВН, высота ∆ АВС, равна 2 см.
S ∆ АВС=ВН•AC:2=8 см²
б) ∆ АВС - остроугольный. Центр О - в плоскости треугольника.
Проведем диаметр СК и соединим К и В.
∆ СВК - прямоугольный ( угол В опирается на диаметр).
ВН в нём - высота, СК - гипотенуза, СН - проекция катета СВ на гипотенузу.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
СН²=ВН•KH⇒
ВH=СН²:HK
НК=10-ВН
16=BH•(10-ВН)
BH²-10 BH+16=0 ⇒
BН₁=8 см; ВН₂=2 см ( это значение мы использовали для тупоугольного треугольника)
S ∆ АВС =8•8:2=32 cм²