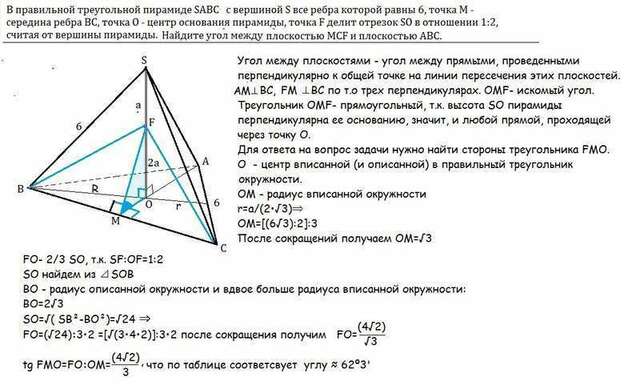
B правильной треугольной пирамиде SABC с вершиной S все ребра которой равны 6, точка М - середина ребра BC, точка О - центр основания пирамиды, точка F делит отрезок SO в отношении 1:2, считая от вершины пирамиды. Найдите угол между плоскостью MCF и плоскостью ABC.
––––––––––––––––
Угол между плоскостями - это угол между прямыми, проведенными перпендикулярно к общей точке на линии пересечения этих плоскостей. АМ⊥ВС, и FM ⊥ ВС по т.о трех перпендикулярах. ОМF- искомый угол.
Треугольник ОМF- прямоугольный, т.к. высота SO пирамиды перпендикулярна ее основанию, значит, и любой прямой, проходящей через точку О.
Для ответа на вопрос задачи нужно найти стороны треугольника FMO.
О - центр вписанной (и описанной) в правильный треугольник окружности.
ОМ - радиус вписанной окружности
r=a/(2•√3)⇒
OM=[(6√3):2]:3
После сокращений получаем ОМ=√3
FO= 2/3 SO, т.к. SF:OF=1:2
SO найдем из ⊿ SOB
ВО - радиус описанной окружности и вдвое больше радиуса вписанной окружности:
ВО=2√3
SO=√( SB²-BO² )=√24 ⇒
FO=(√24):3•2 =[√(3•4•2)]:3•2 после сокращений получим
FO=(4√2):√3
tg FMO=FO:OM=(4√2):3, что по таблице соответсвует углу ≈ 62º3'