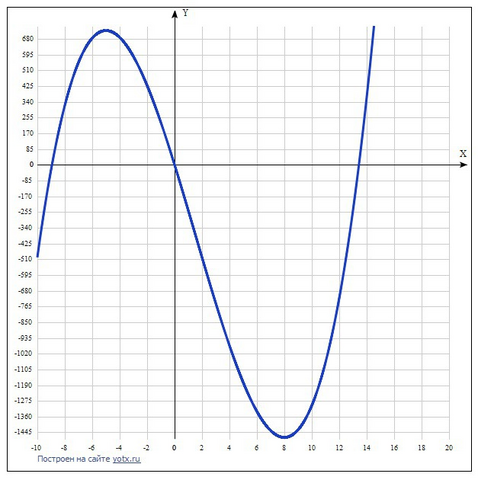
23) Дана функция f(x) = 2x³ - 9x² -240x.
Находим производную и приравниваем её нулю:
f'(x) = 6x² - 18x - 240 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-18)^2-4*6*(-240)=324-4*6*(-240)=324-24*(-240)=324-(-24*240)=324-(-5760)=324+5760=6084;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√6084-(-18))/(2*6)=(78-(-18))/(2*6)=(78+18)/(2*6)=96/(2*6)=96/12=8;
x_2=(-√6084-(-18))/(2*6)=(-78-(-18))/(2*6)=(-78+18)/(2*6)=-60/(2*6)=-60/12=-5.
Это найдены критические точки.
Исследуем поведение производной вблизи критических точек.
х =
-5.5
-5 -4.5 7.5 8 8.5
у' =6x^2-18x-240 40.5
0 -37.5 -37.5 0 40.5.
Функция убывает, где производная отрицательна, то есть на промежутке: -5
24) Площадь основания равна So = (1/2)d1*d2 = (1/2)*6*8 = 24.
Сторона основания равна 5 (как гипотенуза при катетах 3 и 4).
Площадь треугольника - половины ромба равна 24/2 = 12.
Высота основания равна h = 2S/b = 2*12/5 = 24/5 = 4,8.
Тогда высота параллелепипеда H = h*tg 60° = 4.8*√3.
Отсюда находим его объём: V = So*H = 24*4.8√3 = 115,2√3 ≈ 199,5323.
25) 7^(x²) = 7^(y-x), x² = y - x, y = x² + x.(1)
x + 4 = y. (2)
Вычтем из первого второе: х² - 4 = 0.
Отсюда х1 = 2, х2 = -2, у1 = 6, у2 = 2.
26) Произведение равно нулю, когда один или все множители равны нулю.
Приравняем 0 первый множитель:
sin(x) - cos(x) = 0.
sin(x) = cos(x).
sin(x) = √(1-sin²(x)).
Возведём в квадрат обе стороны уравнения:
sin²(x) = 1-sin²(x),
2sin²(x) = 1,
sin(x) = √(1/2) = 1/√2 = √2/2.
х = (π/4)+2πk, x = (3π/4)+2πk, k ∈ Z.
sin(x) = -√2/2.
х = (-π/4)+2πk, x = (-3π/4)+2πk, k ∈ Z.
Приравняем 0 второй множитель:
log(2,(5-x²)) = 0.
Это то же самое: 2^0 = 5-x²,
5-x² = 1,
x² = 4,
x = 2,
x = -2.