В треугольнике АВС высота ВН, равная 6, и медиана СМ, равная 5, пересекаются в точке О....

Question

В треугольнике АВС высота ВН, равная 6, и медиана СМ, равная 5, пересекаются в точке О. Расстояние от точки О до стороны АС равно 1. Найдите сторону ВС.

Comments

я пытаюсь, но что-то у меня не сходится, черт подери.

---

спасибо, за старания )

---

Из принципа буду ща добивать.

---

Расстояние от M до АС равно 3. Значит О делит CM в отношении 2:1. Дальше все легко.

---

Почему расстояние от м до ас равно 3, если в условии не сказано. что м половина от высоты...

---

М - середина AB, а это и значит, что расстояние от нее до АС равно половине высоты

---

Ничего не понимаю, разве может медиана влиять вот так на высоту

---

Проведите среднюю линию тр-ка АBC параллельную AC. Она делит высоту пополам (т.к. является и средней линией тр-ка ABH). Расстояние от любой ее точки до основания равно половине высоты. В том числе и расстояние от М, которая лежит на этой средней линии.

---

а ожно решение до конца?

---

можно*

Answer 1

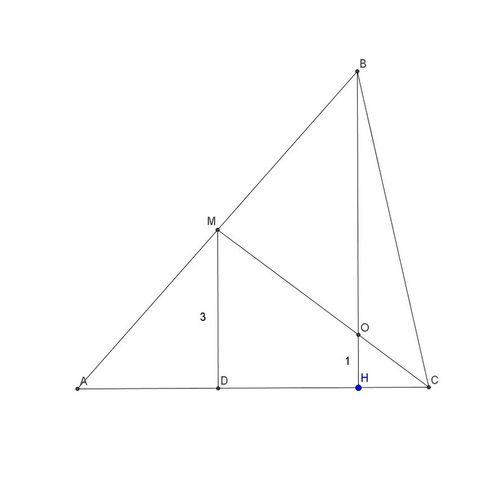
Пусть MD - высота треугольника AMC, тогда MD - средняя линия треугольника ABH (т.к. М - середина AB и MD||BH), т.е. MD=BH/2=3.
Треугольники HOC и DMC подобны с коэфф. подобия OH/MD=1/3. Значит, OC=СM/3=5/3. По т. Пифагора HC²=OC²-OH²=(5/3)²-1=16/9.
BC=√(HC²+BH²)=√(16/9+6²)=(2√85)/3.

---