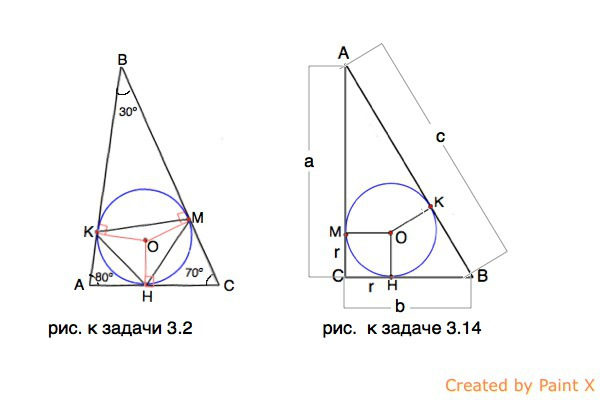
3.2 В треугольник с углами 30º, 70º, и 80º вписан круг. Найти углы треугольника, вершины которого являются точки касания вписанного круга со сторонами данного треугольника.
Пусть в треугольнике АВС угол А=80º, угол В=30º, угол С=70º
Точки касания: на АВ-К, на ВС- М, на АС - Н; центр круга - О.
Соединим центр круга с точками касания.
Радиусы ОК, ОМ, ОН, проведенные в точки касания перпендикулярны сторонам ∆ АВС и образуют с ними углы 90º.
Сумма углов четырехугольника 360º.
Отсюда в четырехугольнике ВКОМ центральный угол КОМ=360º-2•90º-30º=150º
Величина вписанного угла КНМ, опирающегося на ту же дугу, равна половине угла КОМ.
Угол КНМ =150º:2=75º
Аналогично в четырехугольнике АКОН угол КОН=100º, а вписанный угол КМН=100º:2=50º
В четырехугольнике МОНС угол МОН=110º, а вписанный угол МКН=110:2=55º
Углы треугольника КМН равны 75º, 50º, 55º, и их сумма равна 180º
________________
3.14. Докажите, что радиус окружности, вписанной в прямоугольный треугольник, выражается формулой r=(a+b-c):2, где r- радиус вписанного круга. а и b - катеты, с - гипотенуза.
Начертим прямоугольный треугольник АВС, центр вписанного круга О, точки его касания со сторонами
на АС-М, на АВ- К, на СВ -Н
Пусть АС=а, ВС=b, АВ=с.А
Для вписанного круга стороны треугольника - касательные.
Отрезки касательных от точки вне круга до точек касания равны.
АМ=АК=а-r, NH+BK=b-r.⇒
AB=с= a-r+b-r=a+b-2r
c=a+b-2r
2r=a+b-c
r=(a+b-c):2, что и требовалось доказать.