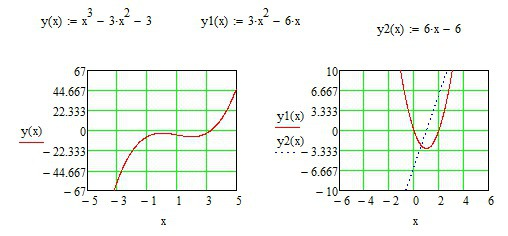
Исследование точек экстремума функции проведём по первой производной функции. Первая производная равна y'(x)=3*x²-6*x, её значения равны нулю х1=0 (производная меняет знак с + на минус, так что эта точка - точка локального максимума) х2=2 (производная меняет знак с минуса на =, так что эта точка - точка локального минимума).
По второй производной исследуем выпуклости и вогнутости. Вторая производная y''(x)=6*x-6, она равна нулю при х3=1, при отрицательной производной у функции выпуклость вверх, при положительной - выпуклость вниз. Графики функций прилагаются.