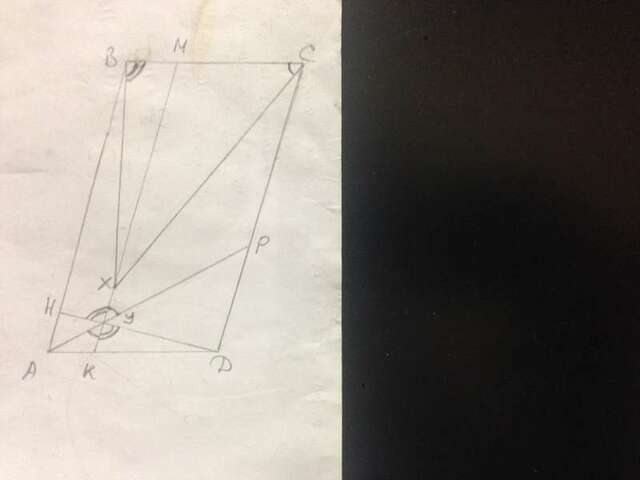
Продолжим отрезок XY до пересечения со сторонами АД и ВС в точках К и М соответственно.
∠XYA+∠XCB=∠XYA+∠XYP=180°, значит ∠XYP=XCB.
∠XYD+∠ХBC=∠XYD+XYH=180°, значит ∠XYH=∠ХBC.
В тр-ках АYK и CXM ∠АYK=∠XCM и ∠AKY=∠CMX как накрест лежащие, значит эти треугольники подобны.
В тр-ках DYK и BXM ∠DYK=∠XBM и ∠DKY=∠BMX как накрест лежащие, значит они подобны.
Пусть АК=х, DK=y, тогда В треугольниках AYK и DYK отношение этих сторон: АК:DK=х:у, а сторона YK у них общая и отношение будет 1:1.
Для сторон АК и DK из тр-ках AYK и DYK в подобных для них тр-ках ВMX и СMX соответственными для них сторонами будет МХ и МХ (она общая с отношением 1:1), а для сторон YK и YK - соответственные стороны СМ и ВМ.
Чтобы привести подобие сторон АК и DK в тр-ках АYK и DYК к такому же подобию, как у общей стороны МХ в тр-ках ВMX и DМХ (1:1), нужно все стороны тр-ка AYK умножить на у, а тр-ка DYK - на х.
АК·у=ху, DK·x=ух. Hовое отношение 1:1, как у сторон МХ в тр-ках ВМX и СMX.
В тр-ке AYK YK·y=y. В тр-ке DYK YK·x=x. Новое отношение получится как у сторон ВМ и СМ в треугольниках ВМX и CMХ: ВМ:СМ=х:у.
В параллелограмме АВCD AD=BC, AD║BC. AK:DK=ВМ:СМ=х:у, значит АК=ВМ и DK=СМ, следовательно АВМК - параллелограмм, в котором АВ║МК.
XY∈МК ⇒ XY║АВ.
Доказано.