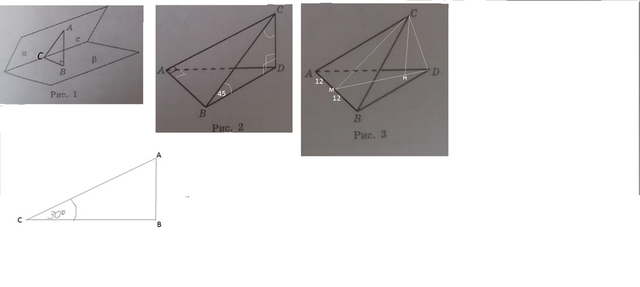
2.
а)
На одной из граней двугранного угла взята точка А
Найдите расстояние от данной точки до ребра угла, если точка отдалена от второй грани на 4√2 см, а градусная мера двугранного угла равна 30º
Рисунок 1 данного в задаче вложения подойдет в качестве ориентира, хотя угол не похож на угол 30º
Обозначим точку проекции А на ребро буквой С
Треугольник АВС - прямоугольный.
Катет АВ= 4√2 см
Гипотенуза АС равна расстоянию от точки А до ребра двугранного угла.
АС=АВ:sin(30º)=8√2 cм
-----------
б) На одной из граней двугранного угла обозначена точка (рис.1). Найдите расстояние от данной точки до второй грани, если данная точка отдалена от ребра угла на 4 см, а градусная мера двугранного угла равна 60º
----------
Треугольник АВС - прямоугольный.
Гипотенуза АС= 4см
Расстояние от данной точки А до второй грани - это катет АВ
АВ=АС∙sin(60º)=(4√3):2=2√3cм
-------------------
в)
На рис. 2 CD⊥(ABD). ∠САВ=90º
Найдите угол между плоскостями АВС и АВD, если СD=5см, АВ=2√5 см, а прямая СВ образует с плоскостью АВD угол 45º.
Искомый угол - это угол САD.
Чтобы его найти, следует найти АD и АС.
По теореме о трех перпендикулярах АD⊥AB, т.к. AD - содержит проекцию АС на плоскость.
Так как угол СВD=45º, DB=CD=5 см
СВ=5√2
Из прямоугольного треугольника DАВ найдем АD
АD=√(DВ²-АВ²)=√(25-20)=√5
АС=√(ВС² - АВ²)=*√(50-20)=√30
sin ∠CAD=CD:AC=5:√30= 5:5,477=0,913
cos ∠CAD=AD:AC=√5:√30=1/√6=1:2,449=0,408
Угол CAD≈ 66º
----
г)
Угол между плоскостями АВС и АВD равен 60º (рис. 3). Найдите СD, если АС=ВС=13см, АВ=24 см,
AD=BD=15 cм
Расстояние от точки до плоскости - это перпендикуляр, опущенный из этой точки на плоскость.
Искомое расстояние равно высоте треугольника MCD - обозначим ее СН.
СН=СМ∙sin(60º)
СМ=5 см ( Пифагорова тройка 12, 13, 5), можно проверить по т.Пифагора, будет та же величина)
СН=5∙sin(60º)=(5√3):2=2,5√3 см