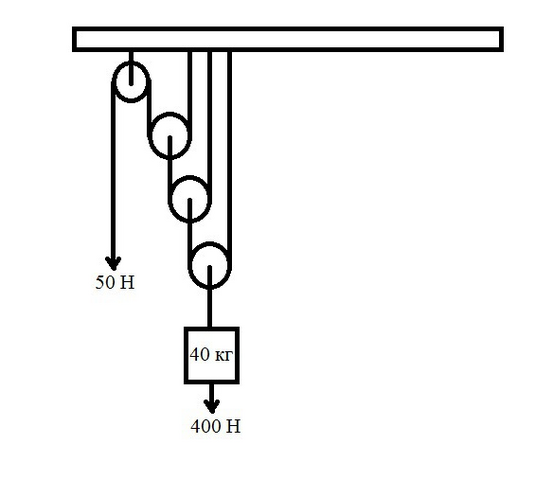
2) сила тяжести груза равна F1=mg. F1=40*10=400 Н. TЕго удерживает сила F2=50 Н.
Выигрыш в силе даёт только подвижный блок, причём в два раза. Отношения сил равны n=F1/F2; n=400/50=8=2^3. Следовательно используется 3 подвижных блока и один неподвижный.
3) Средняя скорость равна v=L/T; v=120/2=60 км/ч.
v1=65 км/ч; v2=55 км/ч; Получаем систему уравнений:
x+y=120;
x/65+y/55=2;
x=120-y;
(120-y)/65+y/55=2;
55(120-y)+65y=2*65*55;
6600-55y+65y=7150;
10y=7150-6600;
y=550/10;
y=55 (км)
x=120-55=65 (км) хороший участок.
4) Будем считать направление "вниз" положительным. На плавающий поплавок будут действовать следующие силы: 1) равнодействующая сил тяжести и Архимедовой силы пластилинового груза F1=(p1-p2)V1g; где p1 и p2 плотности пластилина и воды соответственно, а V1 - объём пластилина.
2) сила тяжести поплавка F2=p3V3g, p3 - плотность пенопласта, V3 - объём поплавка V3=0.1*(5*10^-5)=5*10^-6 (м^3)
3) Архимедова сила поплавка F3=-p2V4g, V4 - объём подводной части поплавка V4=0.075*(5*10^-5)=3.75*10^-6 (м^3).
Условие равновесия системы F1+F2+F3=0;
(p1-p2)V1g+p3V3g-p2V4g=0; Так как V1=m1/p1 получим формулу, из которой найдём массу пластилина m1:
m1-m1(p2/p1)+p3V3-p2V4=0;
m1(1-p2/p1)+p3V3-p2V4;
m1=-(p3V3-p2V4)/(1-p2/p1);
m1=-(50*5*10^-6 (м^3)-1000*3.75*10^-6)/(1-1000/1500);
m1=0.0105 кг (10,5 г)