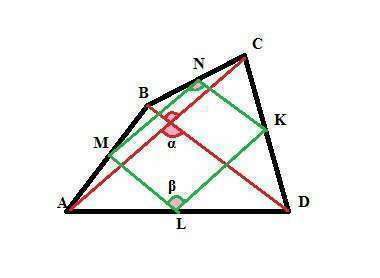
Четырехугольник MNKL - параллелограмм, так как MN и KL средние линии треугольников АВС и АDС. Они равны (1/2) диагонали АС и параллельны ей. Точно также ML и NK - средние линии треугольников АВD и CBD. Они равны (1/2) диагонали ВD и параллельны ей.
Площадь четырехугольника равна половине произведения диагоналей и синуса острого угла между ними.
Таким образом, Sabcd=(AC*BD*Sinα)/2.
Площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Smnkl=MN*NK*Sinβ. Но угол β равен углу α, как углы с параллельными соответственными сторонами.
Тогда Smnkl=[(AC/2)*(BD/2)*Sinα].
Отношение Sfdcd/Smnkl=[(AC*BD*Sinα)/2]/[(AC/2)*(BD/2)*Sinα]=2, то есть площадь четырехугольника MNKL равна половине площади четырехугольника АВСD, что и требовалось доказать.