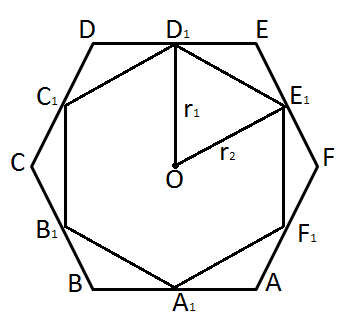
Сторона правильного шестиугольника, вписанного в окружность, равна стороне одного из 6 правильных треугольников, сторона которых равна радиусу описанной окружности. Пусть она равна
а
Сторона правильного шестиугольника, описанного вокруг окружности того же радиуса, равна
2(а√3):3
Отношение этих сторон ( крэффициент подобия) равно
а:2(а√3):3=3а:2(а√3)
Таков же коэффициент подобия их периметров.
Отношение площадей многоугольников равно квадрату коэффициента их подобия.
(3а:2(а√3 )²=
9а²:4а²3
=3/4