Вектор буду обозначать значком "¬"
АВ¬*ВС¬ - называется скалярное произведение векторов. Найдем его по формуле
а¬*b¬ =|a|*|b|*cosα,
где |a| и |b|-длины векторов а и b соответственно, α-угол между этими векторами. (чтобы найти угол, векторы должны выходить из одной точки)
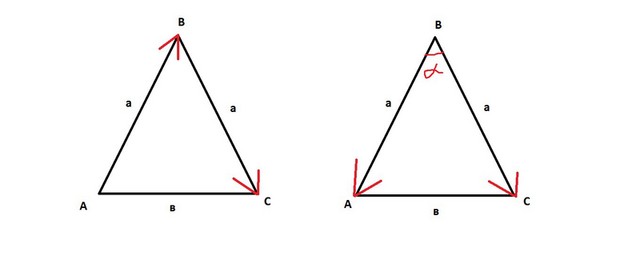
на рисунке на левом треугольнике показаны векторы АВ и ВС, тогда
АВ¬*ВС¬=|AB|*|BC|*cosα
но угла между ними не видно, так как они не выходят из одной точки.
Поэтому заменим вектор АВ на вектор -ВА
теперь векторы ВС и ВА выходят из одной точки В, значит угол между ними α=∠АВС (см. правый треугольник)
-ВА¬*ВС¬=|AB|*|BC|*cosα |*(-1)
ВА¬*ВС¬= -|AB|*|BC|*cosα
мы не знаем cosα, найдем по теореме косинусов
АС²=АВ²+ВС²-2АВ*ВС*cosα
b²=a²+a²-2a*a*cosα
b²=2a²-2a²*cosα
2a²*cosα=2a²-b²
cosα=(2a²-b²)/2a²
ВА¬*ВС¬= -|AB|*|BC|*cosα=-a*a*(2a²-b²)/2a²=-a²(2a²-b²)/2a²=-(2a²-b²))/2=(b²-2a²)/2
отв: (b²-2a²)/2