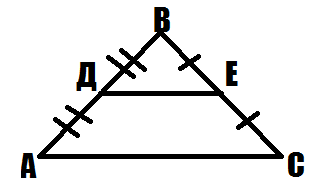
Решение:
1) Проведем прямую ДЕ, которая будет являться средней линией треугольника АВС, т.к. Д и Е - середины сторон.
2) Средняя линия треугольника равна половине параллельной стороны (то есть половине АС), ДЕ = 44 : 2 = 22 (см.)
3) Д - середина АВ по условию. АД = ДВ = 1/2 АВ, АД = 24 : 2 = 12 (см.)
4) Е - середина ВС по условию. ЕВ = ЕС = 1/2 ВС, ЕС = 32 : 2 = 16 (см.)
5) Периметр четырехугольника АДЕС = АС + ЕС + АД + ДЕ = 44 + 16 + 12 + 22 = 94 (см.)
Ответ: Периметр четырехугольника АДЕС = 94 см.