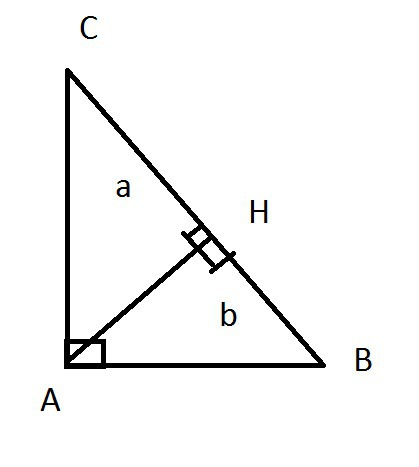
Назовем наш треугольник АВС(А=90*) - высота АН, основание/гипотенуза ВС, АС и АВ - катеты
Данная высота это среднее пропорциональное между проекциями катетов на гипотенузу :
АН^2=BH*CH (дальше для упрощения записи а и b)
система:
a-b=7
a*b=12^2
выразим из первого уравнения "а"
a=7+b(подстановка)
подставим во второе
b*(7+b)=144
b^2+7b-144=0 - это приведенное уравнение
по т виета
b1+b2=-7
b1*b2=-144
b1=-16 (<0, не подходит)<br>b2=9 (отрезок ВН)
подставляем то,что у нас получилось, в подстановку
а=9+7
а=16( отрезок СН)
АС=16+9
АС=25 (гипотенуза)
Далее рассмотрим треугольники , на которые делит большой треугольник высота - АВН и АСН
1)Они также прямоугольные (т.к высота с основанием образует угол в 90*)
2)Нам в них известны оба катета :
В треугольнике АВН: АН=12, ВН=9,
В треугольнике АНС: АН=12, СН= 16
По т. Пифагора найдем АВ и АС(гипотенузы данных треугольников)
в треугольнике АВН
АВ= корень из (AH^2+BH^2)
АВ= корень из (12^2+9^2)
АВ= корень из (144+81)
АВ= корень из (225)
АВ=15
в треугольнике АНС
АС= корень из (AH^2+СH^2)
АС= корень из (12^2+16^2)
АС= корень из (144+256)
АС= корень из (400)
АС= 20
Периметр это сумма всех сторон треугольника
Р=АС+ВС+АВ
Р=20+15+25
Р=60