Диагональ равнобокой трапеции перпендикулярна боковой стороне, а проекция этой диагонали...

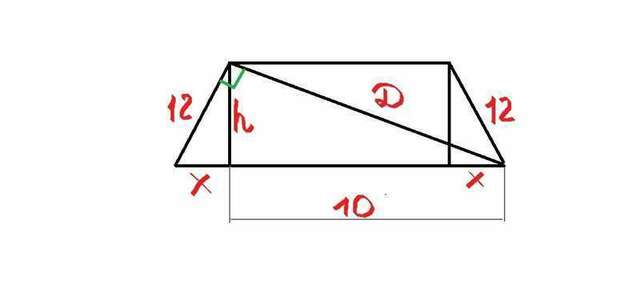
Исходя из русунка в приложении получаем:

$D=\sqrt{(10+x)^2-12^2}$

$h=\sqrt{12^2-x^2}$ $h=\sqrt{D^2-10^2}$

Откуда получаем

$12^2-x^2=D^2-10^2$

Подставляя D в формулу получаем:

$12^2-x^2=(10+x)^2-12^2-10^2$

$100+20x+x^2-144-100-144+x^2=0$

$2x^2+20x-288=0$

$x^2+10x-144=0$

$x_1=8$

$x_2=-18$ этот вариант не подходит ввиду невозможности отрицательной длины

Тогда нижнее основание равно $10+x=10+8=18$

Высота равна: $h=\sqrt{144-x^2}=\sqrt{144-64}=\sqrt{80}$

Так как трапеция равнобокая, то исходя из рисунка получаем, что верхнее основание равно 2

Ответ: 2,18, $\sqrt{80}$