Противоположные стороны AD и BC четырёхугольника ABCD параллельны. Через вершины B и D...

Question

Противоположные стороны AD и BC четырёхугольника ABCD параллельны. Через вершины B и D проведены параллельные прямые, пересекающие диагональ AC в точках M и N соответственно. Оказалось, что AM=MN=Nc/
а) Докажите, что ABCD - параллелограмм.
б) Найдите отношение площади четырёхугольника BMDN к площади параллелограмма ABCD.

Answer 1

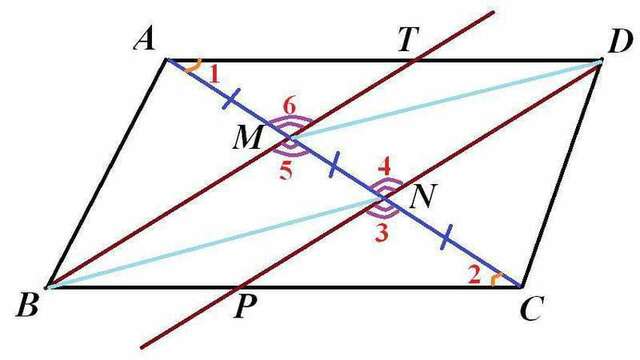
Чертеж - во вложении.
а) Докажем, что АВСD - параллелограмм.
1) Рассмотрим Δ АМТ и Δ ВМC. Они подобны по двум углам, т.к. ∠1=∠2 (накрест лежащие при AD||BC и секущей АС), ∠5=∠6 (вертикальные). Следовательно, АМ:МС=АТ:ВС.
Т.к. по условию АМ=МN=NC, то АМ:МС=1:2 ⇒ АТ:ВС=1:2 ⇒ ВС=2АТ.
Аналогично, подобны Δ PNC и Δ AND. Поэтому AD=2PC.
2) Т.к. BM||DP и АС - секущая, то ∠3=∠4=∠5=∠6.
3) Δ АМТ = Δ PNC (по стороне и прилежащим углам: АМ=NC, ∠1=∠2, 
∠3=∠6) ⇒ АТ=РС ⇒ ВС=AD.
Вывод: т.к. по условию ВС||AD и по доказанному BC=AD, то по признаку ABCD - параллелограмм. 
Доказано.
б) Диагональ АС делит параллелограмм ABCD на два треугольника АВС и ADC с равными площадями.
В Δ АВN ВМ - медиана ⇒  
Аналогично, 

Ответ: 

---

---