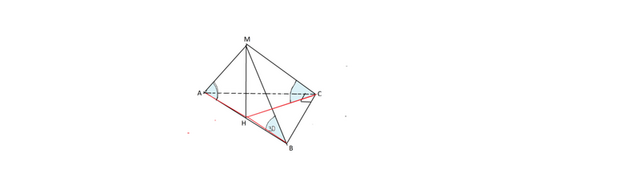
По свойству пирамиды основание её высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
Даю довольно подробное решение, думаю, это не будет лишним.
Каждое ребро пирамиды - это наклонная и является гипотенузой прямоугольного треугольника, катетами в котором являются высота пирамиды и проекция ребра на основание.
Высота одна и та же для всех этих треугольников, - это высота самой пирамиды, она противолежит углу 30° и потому ребра пирамиды, как гипотенуза каждого из этих треугольников, равны двум высотам пирамиды и равны между собой.
Проекции этих наклонных - ребер пирамиды - равны медиане СН, равны и половине гипотенузы треугольника в основании пирамиды,( свойство медианы прямоугольного треугольника) и с ребрами по условию составляют угол 30°
Высота пирамиды имеет основанием середину Н гипотенузы АВ этого прямоугольного треугольника.
Гипотенузу АВ найдем по теореме Пифагора, но заранее можно сказать, что гипотенуза равна 10 см ( треугольник египетский).
АВ=√(8²+6²)=10 см
ВН=АВ:2=5 см
ВМ=АМ=СМ=ВН:cos 30°= 5*2: √3=10√3):3 = ≈5,77 см