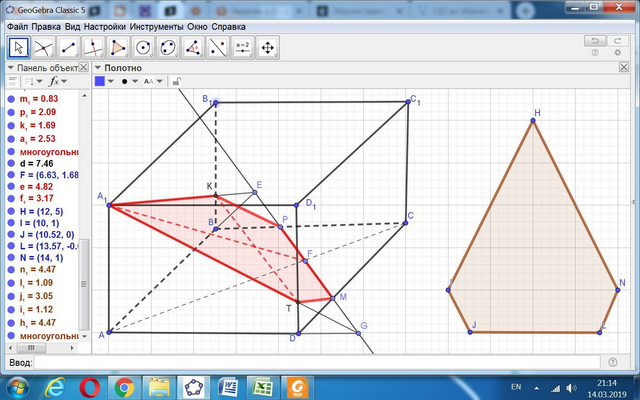
В сечении получаем пятиугольник, который для определения площади можно разделить на равнобедренные треугольник и трапецию. Основание РМ этой фигуры равно 6√2.
Заданная плоскость пересекает рёбра ВВ1 и ДД1 в точках К и Т, расстояние между которыми равно диагонали квадрата основания, то есть 8√2.
Отрезок А1F является суммой высот указанных фигур.
Отрезок СF равен как высота из прямого угла 6*6/(6√2) = 6/√2 = 3√2.
Отсюда находим А1F = √(4² + (8√2 - 3√2)²) = √(16 + 50) = √64 = 8.
Расстояние (из подобия) ДТ = (2*4/(8 + 2) = 8/10 = 4/5.
Высота трапеции равна ДТ/cos(A1FA) = (4/5)/(4/8) = 8/5.
Тогда высота треугольника равна 8 - (8/5) = 32/5.
Получаем ответ: S = (1/2)*(32/5)*8√2 + ((8√2 + 6√2)/2)*(8/5) =
= ((32/5)*4√2 + 56√2)/5 = (184√2)/5 кв.ед.