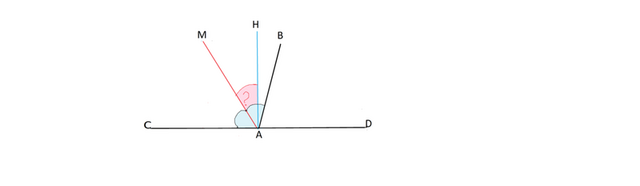
Углы CAВ и BAD смежные.
Найти величину угла между перпендикуляром, проведенным из точки A к прямой CD и биссектрисой угла CAB, если ∠ CAB -∠ ВAD=20°
-------------------------------------------------------------------------------------------
Сделаем рисунок и рассмотрим его.
∠ САВ+∠ВАD=180° - они смежные.
Пусть ∠ САВ=х , тогда ∠ ВАД=180°-х
х-(180-х)=20°
2х=200°
х=100°
∠САВ=100°
∠ВАD=80° ( и разница между ними 20°)
Проведем биссектрису АМ угла САВ.
∠САМ=100°:2=50°
Возведем из точки А перпендикуляр АН к прямой СD.
∠САН =90°
∠САН -∠САМ=90°-50°=40°
Ответ: Искомый ∠ МАН равен 40°