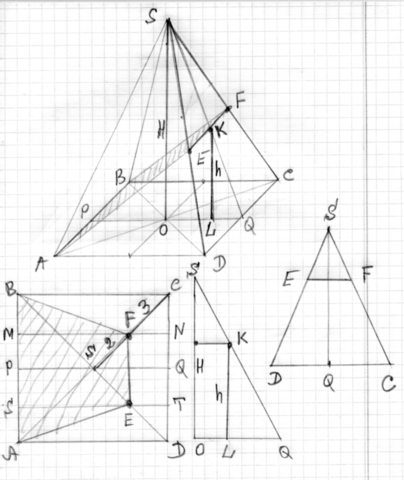
На рис. изображена сама пирамида, вид сверху, треугольник в вертикальном сечении пирамиды и грань DSC.
Заметим, что от выбранных масштабов по осям результат не зависит, поэтому можно просто задать произвольные значения длинам сторон основания и ребрам.
Примем SC=SD=SA=SB=5, AB=BC=CD=DA=2
Тогда SF=SE=2, FC=ED=3
QC=CD/2=1 OQ=PQ/2=DA/2=1
Найдем SQ=sqrt(SC^2-QC^2)=sqrt(25-1)=sqrt(24)=2*sqrt(6)
Найдем высоту пирамиды H=SO=sqrt((SQ^2-OQ^2)=sqrt(24-1)=sqrt(23)
H=sqrt(23)
Найдем объем пирамиды V=(1/3)*AD*DC*SO=(1/3)*2*2*sqrt(23)=(4/3)*sqrt(23)
V=(4/3)*sqrt(23)
Заметим, что сечение разбивает пирамиду на верхнюю наклонную пирамиду и нижний многогранник, который состоит из двух пирамид FMBCN, ESADT и лежащую на боку призму TSENFM (разбиеним вертикальными сечениями по MN и ST).
Найдем объемы этих тел. Для этого нужно вычислить высоту h=KL.
Из подобия тругольников следует, что h/H=KQ/SQ=3/5
h=(3/5)*H=(3/5)*sqrt(23)
h=(3/5)*sqrt(23)
Далее найдем MS=EF и BM=SA
Опять из подобия треугольников EF/DC=SF/SC=2/5
EF=(2/5)*DC=4/5
EF=MS=4/5
SA=(AB-MS)/2= (2-(4/5))/2=3/5
SA=3/5
Объем призмы TSENFM= площадь основания (тр-ка SET) * высоту (MS=EF)
площадь тр-ка SET= (1/2)*ST*h=(1/2)*2*(3/5)sqrt(23)=(3/5)sqrt(23)
Объем призмы TSENFM = (3/5)sqrt(23)*(4/5)=(12/25)*sqrt(23)
Объем призмы TSENFM = (12/25)*sqrt(23)
Найдем объем пирамиды EASTD.
объем пирамиды EASTD=(1/3)*(площадь ее основания) * (ее высоту)
высота пирамиды EASTD=KL=h
площадь основания пирамиды EASTD = AD*SA=2*(3/5)=6/5
объем пирамиды EASTD=(1/3)*(6/5)*(3/5)sqrt(23)=(6/25)*sqrt(23)
Объем пирамиды EASTD=(6/25)*sqrt(23)
Объем нижнего многогранника = объем призмы + 2*(объем пирамиды)
Объем нижнего многогранника = (12/25)*sqrt(23) + 2*(6/25)*sqrt(23) = (24/25)*sqrt(23)
v = Объем верхней отсеченной пирамиды = Объем всей пирамиды SADCD - Объем нижнего многогранника
v=(4/3)sqrt(23) -(24/25)*sqrt(23)=(28/75)*sqrt(23)
v=(28/75)*sqrt(23)
v/V=((28/75)*sqrt(23)) / ((4/3)sqrt(23))=(28/75) / (4/3) =7/25
Ответ: 7/25