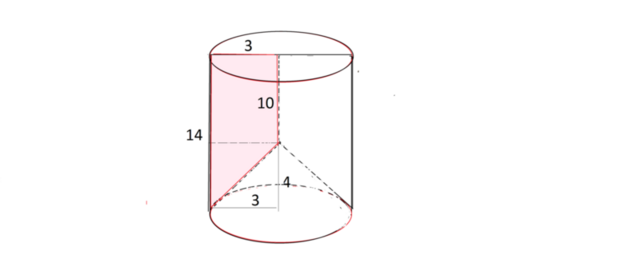
Тело, получившееся при вращении трапеции вокруг своего меньшего основания -
цилиндр, в одном из основании вырезан конус.
Объем этого тела равен объему цилиндра без объема конуса.
Объем цилиндра равен произведению площади основания на высоту.
Радиусом основания является меньшая боковая сторона трапеции,
которая с основаниями трапеции образует прямой угол - трапеция прямогольная по условию задачи, и является ее высотой.
S осн= πr²=π3²=9π см ²
Высотой цилиндра является большее основание трапеции
Высота цилиндра равна 14 см
Найдем объем цилиндра, не учитывая объема "вырезанного" из него конуса.
V=Sh=9π ·14=126π см³
Для того, чтобы найти объем тела вращения, следует найти объем конуса по формуле
Vкон=Sh:3
Площадь основания этого конуса та же, что площадь основания цилиндра, высота равна разности оснований трапеции
h=14 -10=4 см
Vкон=Sh:3=9π·4:=36π:3 =12πсм³
Объем тела вращения
Vцил -Vкон=126π-12π=114 π см³ или ≈ 358,14см³( на π умножено в калькуляторе без сокращения)
-----------------------------------