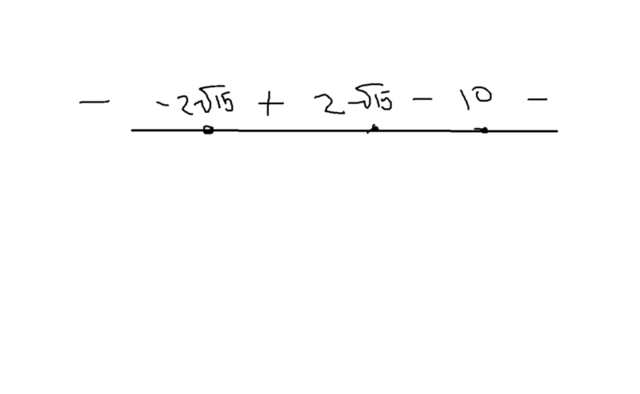Пожалуйста , решите с ОБЪЯСНЕНИЕМ. задания на фото

$1) (12\frac{1}2)^4(\frac{2}{25})^{14}(0,08)^{-11}=(\frac{25}2)^4(\frac{2}{25})^{14}(\frac{2}{25})^{-11}=(\frac{2}{25})^{-4}(\frac{2}{25})^{14}(\frac{2}{25})^{-11}=$

$=(\frac{2}{25})^{-4+14-11}=(\frac{2}{25})^{-1}=\frac{25}2$

Число обратное данному: $\frac{2}{25}$

$\frac{(x^2+10)(x+10)^2}{60-x^2}\geq0$

$x^2+10=0$ - корней не имеет

$(x+10)^2=0$ - корень x=-10

$60-x^2=0$ - корни $x=2\sqrt{15};x=-2\sqrt{15}$

Решаем методом интервалов(см.вложение)

Целые решение: -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Ответ: 13.

$|x-4|+|x+2|-1$

Так как x e [-1;3] , то посмотри, как раскрывается модуль(если модуль <0, то он расрывается отрицательно, елси >0, то расрывается положительно)

Получим: $-x+4+x+2-1$

$6-1$

$5$

Пожалуйста , решите с ОБЪЯСНЕНИЕМ. задания ** фото