К окружности, радиус которой равен 3, из точки, удалённой от центра окружности **...

Question

К окружности, радиус которой равен 3, из точки, удалённой от центра окружности на расстояние 5, проведены две касательные. Вычислите расстояние между точками касания.

Answer 1

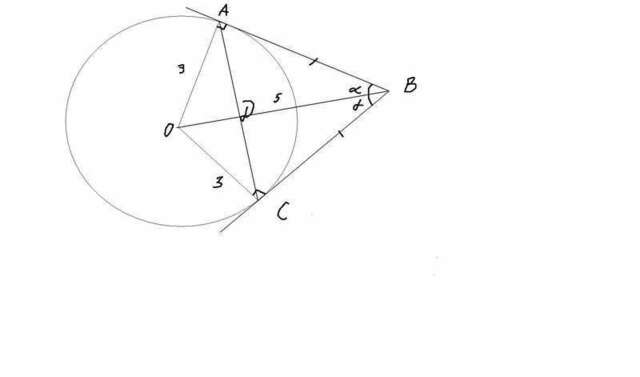
Если я правильно понял рисунок такой 

AB^2=AO^2+BO^2

AB=V5^2-3^2=4

теперь по теореме синусов найдем косинус угол

5=3/sina

3/5=sina

cosa=V1-(3/5)^2=V25-9/25=4/5

a=arccos(4/5)

угол ABC=2arccos(4/5)

по теореме  косинусов  АС^2=2AB^2-2AB^2*cosABC

AC=V32-32*cos(2arccos(4/5))

arccos(4/5)=b

cos(2b)=2cos^2(b)-1=2cosb*cosb -1=2*4/5*4/5-1=7/25

AC=V32-32*7/25=4.8

Значит   4,8

 

 

---