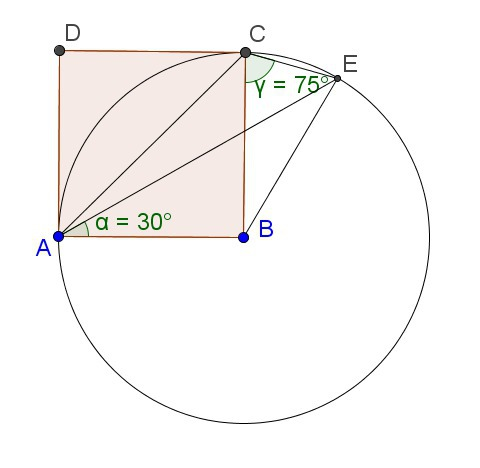
∠AEC=180°-∠CAE-∠ACE=180°-(45°-30°)-(45°+75°)=45°
Проведем окружность с центром B и радиусом равным стороне квадрата. Т.к. ∠AEC=1/2∠ABC (т.е. ∠AEC равен половине центрального угла), то ∠AEC - вписанный, т.е. точка E лежит на окружности. Значит BC=BE как радиусы. Т.е. треугольник BCE - равнобедренный, и значит ∠CBE=180°-2·75°=30°.