Расстояние от точки до плоскости измеряется отрезком, перпендикулярным к плоскости.
Если расстояние от точки вне плоскости квадрата до всех его сторон равно, то проекции на плоскость квадрата наклонных, определяющих это расстояние, равны.
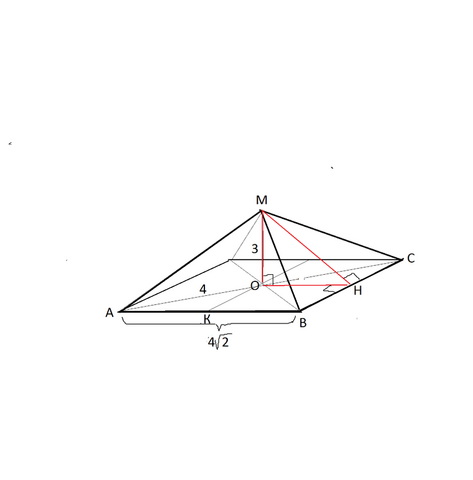
Следовательно, основание отрезка от А до плоскости квадрата лежит в его центре, т.е. точке пересечения диагоналей.
Найдем сторону квадрата.
АС=8,
АО=4,
АВ=4√2
Следовательно, проекция ОН наклонной МН на плоскость квадрата равна половине стороны квадрата и равна 2√2
МН - расстояние от М до сторон квадрата найдем по т. Пифагора:
МН=√(МО²+ОН²)= √(2√2)²+3²)=√17