В правильной треугольной пирамиде боковое ребро, равное b, наклонено к основанию под...

Question

В правильной треугольной пирамиде боковое ребро, равное b, наклонено к основанию под углом a. Через вершину пирамиды параллельно стороне основания проведено сечение, наклоненное к плоскости основания под углом B. Определить площадь сечения.

Answer 1

Для начала замечу, что сечение может быть расположено как между высотой и основанием, так между высотой и ребром.

Принцип решения один и тот же. 

--------------------------------------------------------------------------

 Из вершины пирамиды проведем наклонную SH  под углом β к плоскости ее основания.

Через Н проведем прямую КЕ║АВ

 

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости

 

АВ- не лежит в плоскости треугольника SKE,  параллельна КЕ, лежащей в этой плоскости, следовательно, плоскость ᐃ КSЕ║АВ

Для решения задачи нужно найти высоту SН и основание KE  ᐃ КSЕ.

Делать это будем по шагам. 

 

SO=b*sin α

 

СО=SC*cos α=b*cos α

 

SH=SO:sin β = b*sin α:sin β

 

OH= SO:tg β= b*sin α : tg β

 

CH=CO+OH= b*cos α + b*sin α : tg β

 

Так как КЕ║АВ, треугольник КСЕ подобен равностороннему АСВ и также является равносторонним.

 

∠НЕС=60°

 

CE=CH:sin (60°)= (b*cos α + b*sin α:tg β)*2:√3

 

KE=CE

 

S ᐃSKE=SH*KE:2

 

S ᐃSKE= 1/2)*(b*sin α:sin β)* (b*cos α + b*sin α:tg β)*2:√3

 

S ᐃSKE = (b*sin α:sin β)* (b*cos α + b*sin α:tg β) :√3 =

S ᐃSKE = b² (sin α:sin β)*(cos α + sin α:tg β) :√3

 --------------------------

 

Answer 2

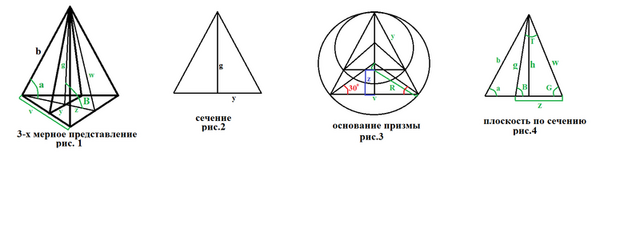
Исходя из геометрии задачи и рисунка 4 в приложении, найдем высоту данной пирамиды:

Так как в основании пирамиды лежит правильный треугольник, найдем радиус его основания, как показано на рисунке 3 в приложении:

Так как треугольник основания правильный, найдем величину радиуса, как показано на рисунке 3, углы при основании прямоугольных треугольника будут равны, тогда длина стороны данного треугольника будет равна:

Так как у правильной пирамиды ребра равны, найдем величину апофемы w, исходя из прямоугольного треугольника бокой грани:

Так как проведенное сечение образует еще одну правильную пирамиду, с правильным треугольником в основании, как показано на рисунке 3, но полученная призма является наклонной, и высоты обеих призм совпадают, тогда можем найти высоту проведенную в сечении (обозначенную буквой g) исходя из рисунка 4:

Тогда используя теорему синусов найдем угол G в том же треугольнике:

Тогда зная углы G и B найдем величину угла T:

Угол B задан в условии а угол G будет равен:

Тогда угол T будет равен:

Тогда исходя из теоремы синусов найдем длину стороны z:

Как показано на рисунке 3 величина z характеризует разность высот обоих треугольников, тогда получаем:

где высота меньшего треугольника, а высота большего треугольника.

Так как треугольники правильные, высота будет вычисляться по формуле:

Получаем:

т.к:

Получаем:

Так как сечение состит из двух прямоугльных треугольников как показано на рисунке 2, тогда его площадь будет равна:

Получаем:

Ответ:

---