конечно можно решить но можно сделать так
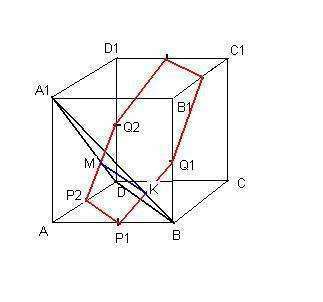
Пересекаются эти сечения по прямой КМ.
Диагонали любой грани куба пересекаются под прямым углом.
Прямая, соединяющая середины сторон, параллельна диагонали грани.
Поэтому она тоже перпендикулярна другой диагонали грани.
Отрезок P1Q1 перпендикулярна A1B. Отрезок P2Q2 перп. A1D.
Вывод: эти сечения перпендикулярны друг другу, угол между ними равен 90.
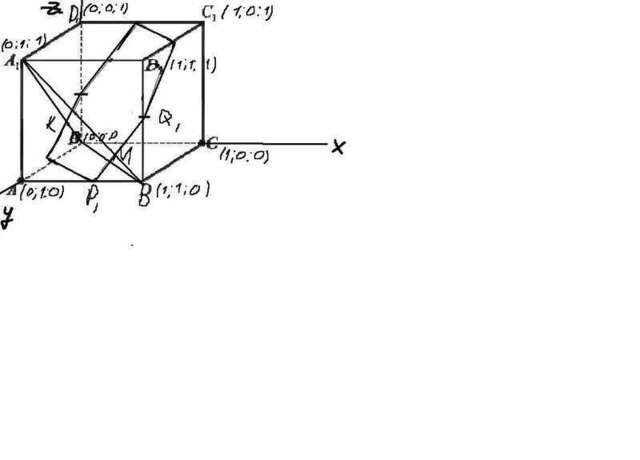
Или решить впишем наш куб в координатую плоскость (x;y;z) то есть сделаем так чтобы ребра были параллельны осям, затем прими все длины граней за 1, тогда
координаты видны на рисунке, надо найти угол между P1Q1 и A1B . Найдем их координаты и вычеслим угол по скалярному произвдению
P1 ( 1/2; 1;0) Q1 (1;1;1/2) и вычтим P1Q1 (1/2;0; 1/2) так же найдем A1B1 (1;0;-1)
теперь по формуле cosa=x1*x2+y1*y2*z1*z2/ на произведение длин !
то есть cosa=(1/2*1+0*0-1/2*1) / √1/2 * √2=0/√1=0
то есть cosa=0
a=90градусов
2 рисунок