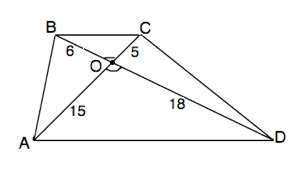
а) В треугольниках ВОС и АОD вертикальные углы при О равны. ОВ:ОD=6:18=1/3;
СО:ОС=5:15=1/3 ⇒ Сходственные стороны ∆ ВОС и ∆ АОD пропорциональны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
Из подобия треугольников следует равенство их накрестлежащих углов. Из равенства накрестлежащих углов при пересечении прямых ВС и АD секущими АС и ВD следует параллельность сторон ВС и AD.
Две стороны четырехугольника АВСD параллельны - это признак трапеции. Доказано.
б) Отношение сторон ∆ ВОС и ∆ АОD равно 1/3, это их коэффициент подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
S ∆ ВОС:S ∆ АОD=k²=1/9