две прямые пересекаются в точке С(-2;-4) найти угол между ними, если одна из них проходит...

Question

две прямые пересекаются в точке С(-2;-4) найти угол между ними, если одна из них проходит через А(1;2), а другая через В(1;-3)

Answer 1

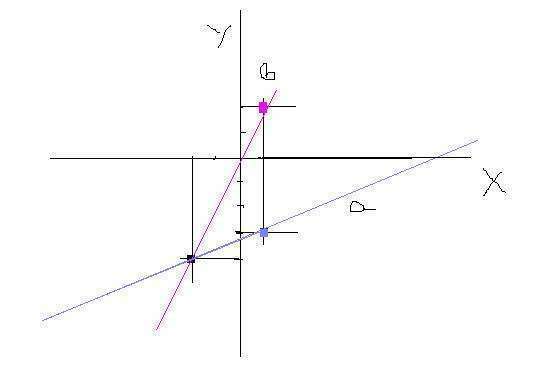
См. рис. во вложении.

Считая точку пересечения О новым началом координат находим координаты направляющих векторов прямых а и в.

Т.е. координаты точки а и в относительно т. О.

Xa=1-(-2)=3

Ya=-3-(-4)=1

Xb=1-(-2)=3

Yb=2-(-4)=6

cos угла=(XaXb+YaYb)/((√(Xa^2+Ya^2)(√(Xb^2+Yb^2)=

=(3*3+1*6)/((√(9+1)(√(9+36)=

=15/√450=15/√(225*2)=15/15√2=1/√2

угол =45 градусов

---