1. Dy=R,
2. Ey=R,
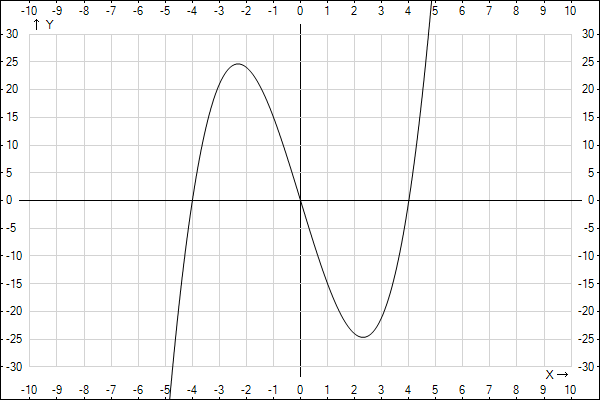
3. x=0, f(0)=0,
f(x)=0, x^3-16x=0,
x(x-4)(x+4)=0,
x_1=0, x_2=4, x_3=-4;
(-4;0), (0;0), (4;0) - пересечение с осями;
4. f(-x)=(-x)^3-16(-x)=-x^3+16x=-(x^3-16x)=-f(x),
нечетная, график симметрчен относительно О;
5. f(x)>0, f(x)<0,</p>
x^3-16x>0,
x(x-4)(x+4)>0,
x∈(-4;0)U(4;+∞) - график над Ох,
х∈(-∞;-4)U(0;4) - график под Ох;
6. f'(x)=3x^2-16,
3x^2-16=0,
x^2=16/3,
x_1=-4/√3=-4√3/3≈-2,3, x_2=4√3/3≈2,3,
f'(x)>0, f'(x)<0,</p>
3x^2-16>0,
(x-4√3/3)(x+4√3/3)>0,
x∈(-∞;-4√3/3)U(4√3/3;+∞) - возрастает,
х∈(-4√3/3;4√3/3) - убывает,
7.f''(x)=6x,
f(-4√3/3)=128√3/9≈24,6,
f(4√3/3)=-128√3/9≈-24,6,
(-4√3/3;128√3/9) - точка максимума,
(4√3/3;-128√3/9) - точка минимума;