Будем использовать следующие известные факты (они все легко доказываются):
1) Угол между биссектрисами двух углов треугольника равен 90° плюс половина третьего угла треугольника.
2) Биссектриса треугольника пересекает его описанную окружность в точке, лежащей на серединном перпендикуляре к той стороне, к которой проведена биссектриса.
3) Вписанный в окружность угол в 60° опирается на хорду равную R√3.
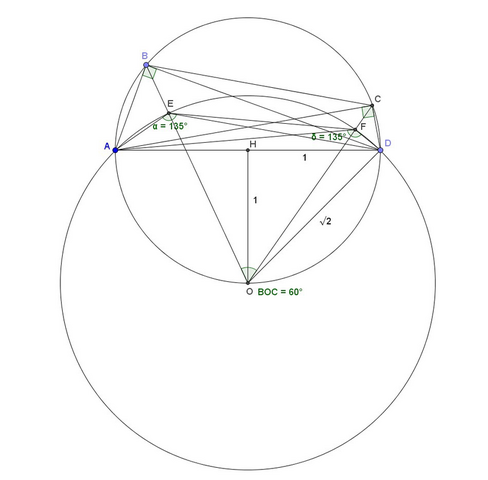
Пусть E и F - точки пересечения биссектрис треугольников ABD и АСD соответственно. Тогда из этих треугольников в силу 1) получаем ∠AED=∠AFD=90°/2+90°=135°. Значит AEFD - вписанный 4-угольник и радиус окружности описанной вокруг него равен AD/(2sin∠AED))=2/(2/√2)=√2=EF. Центр О этой окружности лежит на серединном перпендикуляре к AD и OH=1 т.к. HD=1 и OD=√2, где H - середина AD. Кроме того, треугольник OEF - равносторонний. С другой стороны, в силу факта 2) прямые BE и CF также пересекаются в точке О, т.к. прямоугольные треугольники ABD и ACD вписаны в окружность с центром H и радиусом HD=1. Таким образом, угол ∠BOC=∠EOF=60°, а значит по свойству 3) BC=√3.